[导语]: 本篇博客将分享求解民航停机位分配问题的一种方法
[问题]: 民航静态停机位分配问题
[算法]: 动态禁忌搜索算法
[语言]: python
[源码]: 👉Zhgaot_GitHub
1 模型构建
1.1 符号变量说明
1.1.1 输入变量
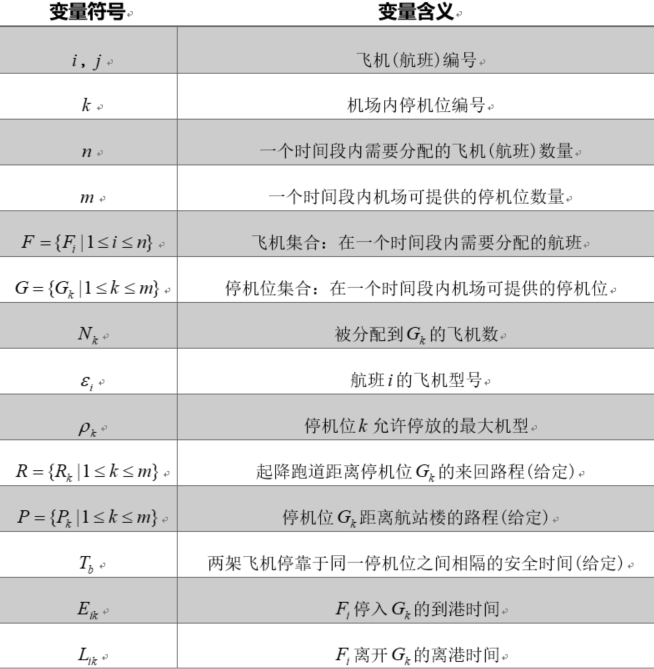
1.1.2 决策变量
1.2 优化目标及目标函数
1.2.1 最小化停机位空间浪费率
停机位的大小要与所停放的飞机机型相匹配，在此暂将机型类比为飞机的大小，即：大型机只能停放在大型停机位，小型机可以停放在大型停机位或小型停机位，但优先为其分配小型停机位。因为机型与停机位不匹配会导致停机位资源的浪费，故为减小这种浪费，将“最小化停机位空间浪费率”作为优化目标之一，它可以表示为：
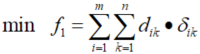
1.2.2 最小化停机位空闲时间——等价于最小化停机位使用数目
在停机位分配过程中，为了尽可能地节省机场空间，增大机场对飞机的容纳程度，应最小化机场停机位的使用数目，它等价于：对每个已参与分配的停机位，最小化空闲时间，使其能尽可能地在一个时间段内多停放飞机。因此，将“最小化停机位空闲时间”作为优化目标之一，它可以表示为：
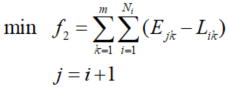
1.2.3 最小化航班在起降跑道至停机位来回路程上的耗能
在飞机对机场的起、降、停行为中，当飞机降落后被分配至某一停机位时，飞机需要从起降跑道移动至停机位，当飞机准备起飞时，飞机需要从停机位移动至起降跑道；同时，飞机的进出方式分为自由/顺序(全发)滑行及顶推(牵引)滑行，它们消耗的能量具有显著差别。为了尽可能地减少飞机在地面上损耗的能量，将“最小化航班在起降跑道至停机位来回路程上的耗能”作为优化目标之一，它可以表示为：
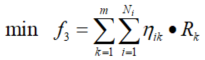
1.2.4 最小化停机位距航站楼的路程
在某些特殊情况（如战时），为使乘客或货物尽快安置在飞机上，提高乘客及货物的安全性，应减少停机位距航站楼的路程，故将此作为优化目标之一，具体可表示为：
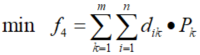
1.2.5 目标函数
综合考虑上述4方面的优化目标，建立同时包含4方面因素的目标函数：
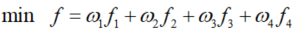
【注意】当前代码中的目标函数仅考虑了 f1 和 f2 两项优化目标。
1.3 约束条件
停机位分配模型的约束条件如下：
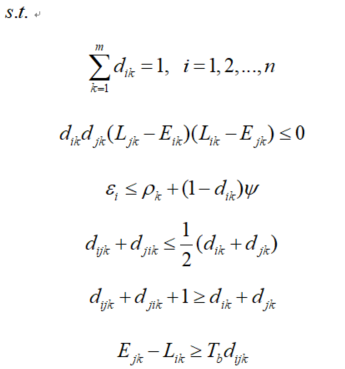
- 每趟航班只能且必须分配一个机场停机位；
- 同一停机位在同一时刻只能停放一架飞机；
- 停机位大小与机型的约束，其中最右侧参数为一个任意大的正数，所有停机位只可停放与其相匹配或小于其大小的机型，即所有停机位只可向下兼容；
- 约束被分配到同一停机位上飞机的先后顺序关系；
- 航班i和航班j为同机位的相邻航班时，两航班间的最小安全缓冲时间约束。
2 动态禁忌搜索算法参数确定
2.1 初始解的产生方法
禁忌搜索算法主要是基于邻域搜索的，故而初始解的好坏直接影响禁忌算法的性能。由于优化目标 f1 在所有情况下均需要纳入最终的目标函数的，因此将其作为初始解的产生依据，即对于满足优化目标 f1 的若干停机位，可随机进行分配，从而产生算法的初始解。这样的初始解有利于更快地找到最优解。
2.2 邻域及候选集合
将“任意交换两趟航班的顺序”作为邻域内的元素，即在当前解序列中任选两趟航班 i, j 进行交换，得到若干个邻域解。对于有 N 趟航班的序列，利用上述方法可以得到的邻域解的个数为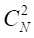
，假如实际场景中 N 值太大，可以随机抽取若干个邻域解，将其中在相同停机位下与前后航班不产生时间冲突的邻域解放入候选集合中，设为 N’ ；如果 N 值不大，则将邻域解中全部在相同停机位下与前后航班不产生时间冲突的邻域解放入候选集合中，此时 N’ = N 。
2.3 评价函数
评价函数是从候选集合元素中选取较优解的一个评价公式，在此，按照通常情况，以目标函数 f 作为评价函数，所有候选集合元素中哪个的目标函数值最小(本算法 minimum 为最优)，且不在禁忌表或满足特设规则时，将其列为当前解序列并放入禁忌表中。
2.4 禁忌表
2.4.1 禁忌对象
被禁止搜索的对象即为禁忌对象，在本算法中为：任意交换两趟航班的顺序。
2.4.2 禁忌表结构
本算法中，禁忌表结构为一个二维数组，用来存储被交换的两趟航班，当 N = 14 时禁忌表的结构如下图所示：
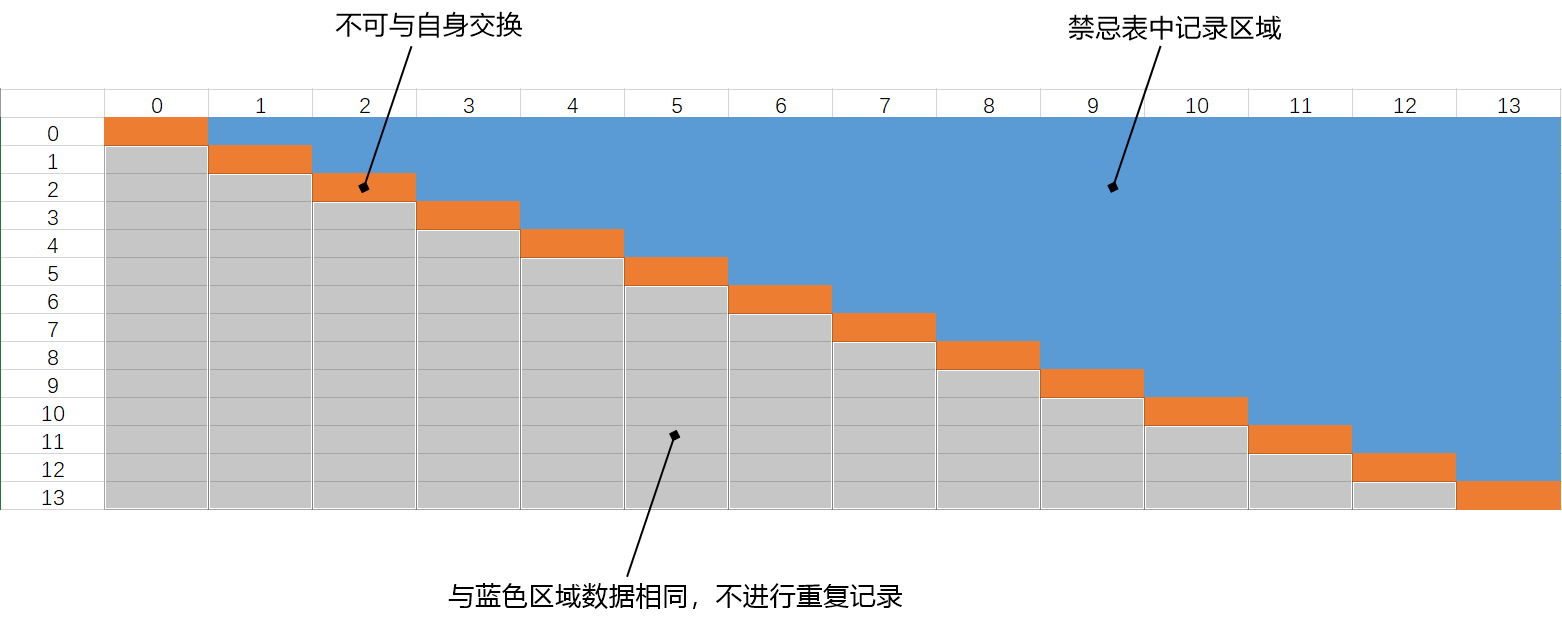
2.4.3 禁忌长度（动态变化）
【注意】当前代码中的暂未实现如下所述的动态禁忌长度
禁忌长度即被禁对象不允许选取的迭代次数，设各个对象的禁忌长度为 LEN 。初始 LEN 值太大可能会造成耗时较长或者算法停止，反之太小则会造成重复搜索、陷入局部最优解，故初始 LEN 的取值范围根据候选集合内的元素个数 N’ 来判定，最佳初始 LEN 值将通过试验测试得到。
另外，各个对象的 LEN 值在本算法中是动态变化的：初始搜索时，为提高解的分散性，扩大搜索区域，使搜索路径多样化，将禁忌表长度设置得尽量小；当搜索过程接近最优解时，为提高解的集中性，减少分散，缩小搜索区域，将禁忌表长度设置得尽量大。
在算法实现中，使用一个二维数组 count 存储每个对象的出现次数，若对象(元素) α 进入禁忌表，则将对象 α 对应的二维数组 count [i] [j] 加1并保存，且根据 count [i] [j] 的值更改对象 α 的禁忌长度 LEN 值(随着 count [i] [j] 越大 LEN 越大)，从而达到约束效果。
对于任一对象来说， count [i] [j] 与 LEN 的关系一定时程正相关，但程正相关的函数有很多，二者遵从的最佳函数是需要通过试验来得出的。例如， count [i] [j] 与 LEN 可遵从如图2所示的各类函数：对数函数、指数函数、一次函数等，其中 LEN 值(y)就近取整。
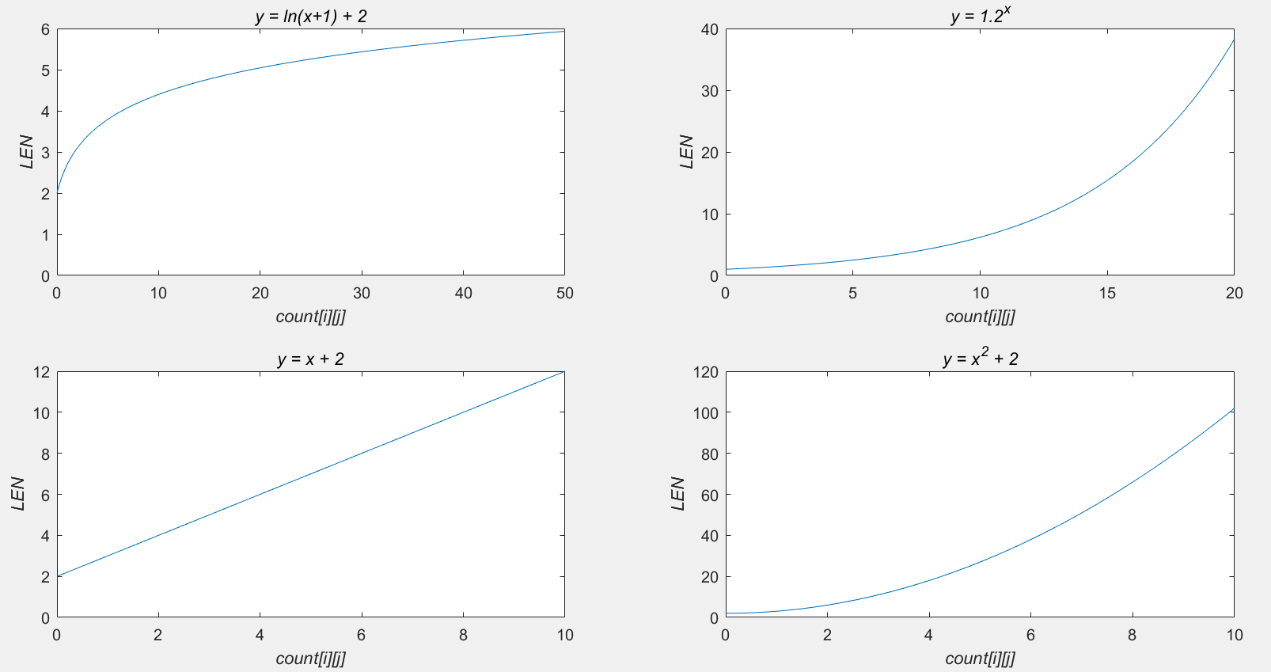
2.5 特赦规则
本算法中的特赦规则为，对于在禁忌表中的对象，若出现以下情况，不论现在对象的禁忌长度是如何，均将其置为0：
- 若出现一个解序列的评价函数值小于前面的最优解序列，可特赦；
- 若所有对象都被禁忌，特赦一个评价函数值最小的解。
2.6 终止规则
因为禁忌搜索算法为一个启发式算法，不可能让搜索过程无穷进行，所以应设置一个终止规则，本算法中设立迭代次数 TIME 作为终止算法的终止规则。
3 算法的输入输出
3.1 算法输入
3.1.1 模型角度
下面给出按照模型角度，算法应输入的参数；当前代码中采用的是3.1.2的输入模式，未来可很容易的将输入功能迁移至配置文件中，在配置文件中直接写明从模型角度的算法输入即可，但当前暂未实现：
- 一段时间内需要分配的飞机(航班)数量：n；
- 机场的停机位类型有几种，各自的停机位数量是多少：m1, m2, …；
- 每趟航班的进港时间、离港时间；
- 飞机型号，停机位型号；
- 两架飞机被安排停靠在同一停机位之间相隔的安全时间；
功能完善后需要追加的算法输入：
- 飞机降落在跑道后到各个停机位的路程、飞机准备起飞时由各个停机位到跑道的路程；
- 各个停机位到航站楼/库房的路程；
- 飞机到不同类型停机位的进出方式及其耗能；
3.1.2 代码角度
可在data/目录中设置：
- 一段时间内需要分配的飞机(航班)数量：Gates；
- 航班数量：Flights；
- 每趟航班的进港时间、离港时间、该航班可停入的停机位编号；
3.2 算法输出
- 在一段时间内，每个停机位都规划停放几架飞机，都是哪几架飞机；
- 为了停放 n 架飞机，共用了几个停机位，都是哪几个；
- 每个被使用的停机位的空闲时间；
- 存在几个冲突，为解决冲突，将哪几各航班分配至停机坪而不是停机位；
